公開鍵暗号方式は、サーバ接続の認証や Web ページの SSL/TLS 通信など、現代の情報セキュリティに欠かせない暗号技術の一つです。
この記事では、まず暗号の歴史を簡単に振り返り、そのうえで公開鍵暗号方式の仕組みと利点を解説します。
さらに、代表的な方式である RSA 暗号の原理をわかりやすく紹介します。
最後に、公開鍵暗号を用いた SSH 接続によるユーザ認証の設定手順を、実際のコマンド例とともに解説します。興味のある方はぜひ最後までご覧ください。
- 暗号に関する簡単な歴史
- 公開鍵暗号方式の仕組み
- RSA暗号の仕組み
- ssh-keygen コマンドの使い方
暗号に関する簡単なまとめ
歴史を振り返ると、人類は暗号を用いて特定の通信文を秘匿するということをやってきました。暗号の技術についてもその時々で新しいものが開発され、現在においても継続されています。この節では、歴史上使われてきた暗号について簡単にまとめたいと思います。
シーザー暗号
まず、暗号の歴史上、最も有名な暗号の一つであるシーザー暗号について説明します。この暗号は、ローマ共和政末期に活躍した政治家であるユリウス・カエサルが発明しました。この暗号は、平文の各アルファベットを辞書順で数文字後ろにずらす(あるいは前にずらす)ことで暗号化します。例えば、各アルファベットを3文字後ろにずらすという規則を用いたシーザー暗号の例は以下のようになります。
平文: I AM HAPPY
暗号: L DP KDSSB
暗号文を受け取った人は、事前に「3文字後ろにずらす」という鍵を用いて復号化ができます。ただし、このシーザー暗号はすべてのアルファベットを同じだけずらすので、高々26回試すことにより鍵を持ってない人でも復号ができてしまいます。
換字式暗号
上記のシーザー暗号は、鍵を持った人以外も容易に復号できてしまうという弱点がありました。この弱点はアルファベットの辞書順で文字を置き換えるという前提があるため発生しています。そこで次に現れるのが、事前に文字の置換表を作り、それに従って文字を置き換えるという手法です。この場合、アルファベットであれば \(26!\) 通り(\(26 \times 25 \times \cdots \times 2 \times 1\)通り)の可能性があり、鍵となる置換表がなければ復号化するのは難しくなります。
この換字式暗号はかなり長い間使用されたようですが、頻度分析という手法を用いて解読されるということが分かりました。この手法は、アルファベットを扱う言語においては、各文字が現れる頻度に偏りがあるため、その偏りを利用する解読手法です。もちろん極端に短い暗号文の場合はこの頻度分析でもどれがどの文字に対応するかはわかりませんが、一定以上長い暗号文の場合は平文を推定することが可能になります。
ヴィジュネル暗号
頻度分析に対抗するために生み出されたのがヴィジュネル暗号です。この暗号は、以下のようなヴィジュネル方陣と呼ばれる表と、情報の送信者、受信者の間で決めておくキーワードを用いて暗号化・復号化を行います:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B: B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C: C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
E: E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F: F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G: G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H: H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I: I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J: J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K: K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L: L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M: M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
N: N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
O: O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
P: P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q: Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R: R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
S: S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T: T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
U: U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V: V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W: W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X: X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y: Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
Z: Z A B C D E F G H I J K L M N O P Q R S T U V W X Y暗号化の方法は、まず一番左側のアルファベットがキーワードとして決めた文字になるように抜き出します。例えば、キーワードとして KEY を指定したなら、上記の表から次の表を抜き出します:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
K: K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
E: E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
Y: Y Z A B C D E F G H I J K L M N O P Q R S T U V W Xそして、平文の最初の一文字目は「K」の行を見て置換、2文字目は「E」の行を用いて置換、3文字目は「Y」の行を見て置換、4文字目は最初に戻って「K」の行を見て置換、といったふうにして暗号化します。
例えば、平文が MATH の場合、上記の KEY の表で暗号化すると WERR となります。復号化する場合は先程とは逆のことをすれば良いです。
ヴィジュネル暗号はかなり強力ですが、人力で暗号化・復号化するにはかなりの労力が必要だったため、開発された当初はそれまで使われていた換字式暗号が依然として使われていたそうです。この強力なヴィジュネル暗号も、19世紀の数学者チャールズ・バベッジにより解読手法が発明されました。
エニグマ暗号
ここでは詳しく説明しませんが、ヴィジュネル暗号の考え方を応用したエニグマ暗号というのが開発され、第二次世界大戦中にドイツ軍が使用していました。こちらも解読するのは不可能と言われていましたが、数学者のアラン・チューリングがエニグマ暗号の弱点を見つけ、解読方法を発見しています。
公開鍵暗号方式
これまで多くの暗号方式が登場してきましたが、いずれの方式でも共通して課題となったのが、「鍵をいかに安全に配送するか」です。どの暗号においても、通信したい相手が正しく読めるようにするには、暗号文と一緒に鍵を届ける必要があり、歴史上の暗号学者を悩ませました。
この鍵配送の問題を解決したのが、公開鍵暗号方式です。この暗号化方式は、公開鍵と秘密鍵という2つの鍵を用いて鍵配送の問題をクリアしました。具体的な方法は以下の通りです。
- 情報の受信者は自分だけで持っておく秘密鍵と、外部に公開する公開鍵を作成する。
- 情報の送信者に公開鍵を渡し、その鍵を用いて情報を暗号化する。
- 暗号化された情報は、秘密鍵で復号化する。
図で書くと、以下のような順序で暗号化・復号を行います。
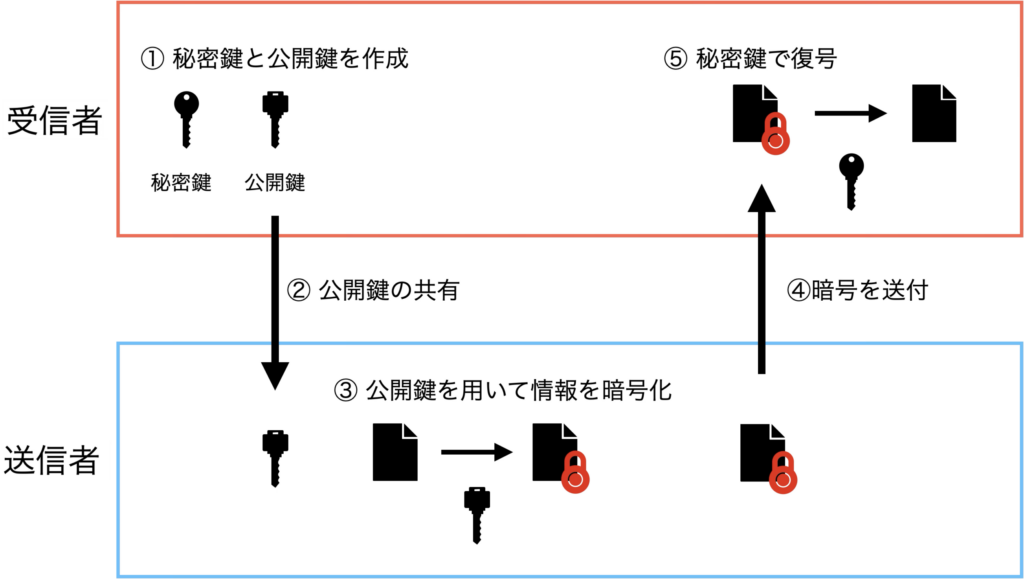
大事な部分としては、復号化のために使う秘密鍵は誰にも渡さないという点です。公開鍵では暗号化された情報を復号することは難しいため、公開鍵に対応する秘密鍵を持っている人しか暗号化された情報を知りえることが基本的にはできません。
以上のことから、公開鍵暗号方式では昔から問題となっていた復号のための鍵の配送をそもそもしなくてよくなったため、鍵配送の問題は解決されました。
ここで「そもそも秘密鍵と公開鍵はどうやって作成するのか」という疑問が出てくると思いますが、これについては以下のような生成アルゴリズムが知られています。
- RSA暗号
- DH法
- 楕円曲線暗号
次の節では、この中でもRSA暗号について原理を解説したいと思います。
RSA暗号
RSA暗号は素因数分解の困難さを安全性の根拠にした暗号になります。与えられた2つの素数を掛けた結果を得ることは簡単ですが、与えられた数の素因数をすべて列挙することは数が大きくなればなるほど難しく、この一方向性を用いています。
ここで、RSAという名前についてはこの暗号の実用化に成功したマサチューセッツ工科大学のロナルド・リヴェスト(Ronald Rivest)、アディ・シャミア(Adi Shamir)、レオナルド・エーデルマン(Leonard Adleman) の名前の頭文字です。
鍵生成の流れ
RSA暗号を用いた秘密鍵と公開鍵の生成の流れについて見ていきます。
- 互いに異なる大きい素数 \(p,\ q\) をランダムに選ぶ。
- \(n = p \times q\) を計算。
- オイラーのトーシェント関数 \(\varphi\) を \(n\) に対して計算する。今回の場合は\(\varphi(n) = (p-1)(q-1)\)である。
- \(1 < e < \varphi(n),\ \mathrm{gcd}(e,\varphi(n)) = 1\) を満たす整数 \(e\) を指定する。ここで、\(\mathrm{gcd} \) は最大公約数を表す関数。
- \(de \equiv 1 \mod \varphi(n)\) を満たす \(d\) を計算する。
- 以上の計算で得られた \((n,e)\) が公開鍵、\((n,d)\) が秘密鍵になる。
- 公開鍵 \((n,e)\) を送信者に共有する。送信者は数 \(M\) を暗号化したい場合、\(C=M^e \bmod n\) を計算し、受信者に送る。
- \(M = C^d \bmod n\) であることに注意すると、受信者は秘密鍵をもっているためこの右辺を計算することで、送信者が送ったメッセージを復元できる。
\(a \bmod b\) は \(a\) を \(b\) で割った余りという意味です。また、\(a \equiv b \mod n\) と書かれた場合、\(a\) を \(n\) で割った余りと \(b\) を \(n\) で割った余りが等しいということを表します。
オイラーのトーシェント関数のきちんとした定義は以下の通りです: 自然数 \(n\) に対して、\(1,2,\ldots,n\) の中にある \(n\) と互いに素な数の個数を \(\varphi(n)\) と表し、このとき得られる関数 \( \varphi \colon \mathbb{N} \to \mathbb{N}\) をオイラーのトーシェント関数といいます。
\(de \equiv 1 \mod \varphi(n)\) を満たす \(d\) の存在は、互いに素な2つの整数に関する次の性質から保証されています: \(a, b\) を互いに素な整数とするとき、\(a x \equiv 1 \mod b\) を満たす \(x\) が \(1 \leq x \leq b-1\) の間でただ一つ存在する。
暗号化と復号の具体例
RSA暗号のアルゴリズムをみたところで、具体的な場合における暗号化と復号についてみていきましょう。
- まず、扱う素数として \(p = 61,\ q = 53\) とします。
- \(n = pq = 61 \times 53 = 3233\) です。
- オイラーのトーシェント関数を計算すると \(\varphi(n) = (61-1)(53-1) = 3120\)となります。
- \(1 < e < \varphi(n),\ \mathrm{gcd}(e,\varphi(n)) = 1\) を満たす整数 \(e\) として、17 を指定します。実際、17と3120は互いに素です。
- \(de \equiv 1 \mod \varphi(n)\) を解きます。今回の場合、この合同方程式は \(17d \equiv 1 \mod 3120\) となりますが、これを満たす \(d\) を拡張ユークリッドの互除法で計算すると2753を得ます。
- 以上から、公開鍵 \((3233,17)\) と秘密鍵 \((3233,2753)\) を得ます。
- 次に平文 \(M=65\) を公開鍵を使って暗号化します。上記の計算に従うと、暗号文 \(C\) は \(C=M^e \bmod n = 65^{17} \bmod 3233\) を得ます。実際に計算すると \(C = 2790\) を得ます。
- 暗号文 \(2790\) を秘密鍵を用いて複合します。\(C^d \bmod n = 2790^{2753} \bmod 3233 = 65\) となります。これは送信者が送ったもとの数 \(M=65\) と一致するため、無事復号できました。
ssh-keygenコマンドを用いた公開鍵暗号方式の実践
Linuxサーバにおいて、公開鍵暗号方式を用いたSSH接続について実践してみましょう。使うコマンドは ssh-keygen というコマンドです。このコマンドを用いることで、上記で見てきた公開鍵と秘密鍵を作成することができます。
事前準備
まずは、テスト用のサーバを用意しましょう。過去の以下の記事でも取り扱ったDockerfileを用いてコンテナを立ち上げてみます。
以下のDockerfileからイメージを作成して、その下のコマンドでコンテナを作成してください。Dockerfileの説明については上記記事をご覧ください。
- Dockerfile
FROM almalinux:latest
RUN dnf -y update \
&& dnf install -y openssh-server
RUN ssh-keygen -A
RUN useradd test-user\
&& echo 'test-user:hogefuga' | chpasswd \
CMD ["/usr/sbin/sshd", "-D"]- Dockerfileからイメージファイルを作成
docker build ./ -t my-alma-ssh- 作成したイメージファイルからコンテナを作成
docker run -d --name ssh-test -p 2222:22 my-alma-sshコンテナの作成までできたら、以下のコマンドでローカルのターミナルからパスワード認証でSSH接続できることを確認します。test-userのパスワードは、「hogefuga」です。
ssh -p 2222 test-user@localhostSSH接続できれば、exitコマンドでログアウトしておきましょう。
秘密鍵と公開鍵の作成
ローカルのターミナルで秘密鍵と公開鍵を作成します。以下のコマンドを実行してみてください。
ssh-keygen -t rsa-t オプションで暗号化方式を定めます。筆者の環境は OpenSSH_9.9p2, LibreSSL 3.3.6 であり、デフォルトでは ed25519 が使われるため、RSAを使うため明示的に指定します。tオプションの引数として使えるは以下のとおりです。
- ecdsa
- ecdsa-sk
- ed25519
- ed25519-sk
- rsa
実行すると、対話形式で入力を促されます。最初に聞かれるファイル名については、空白で実行すると ~/.ssh/id_rsa というファイルが作られてしまい、すでにある場合は上書きされるため、テスト用のファイル名を指定します。
$ ssh-keygen -t rsa
Generating public/private rsa key pair.
Enter file in which to save the key (/Users/hoge/.ssh/id_rsa): id_rsa_test
Enter passphrase for "id_rsa_test" (empty for no passphrase):
Enter same passphrase again:
Your identification has been saved in id_rsa_test
Your public key has been saved in id_rsa_test.pub
The key fingerprint is:
SHA256:EfIfaUNorQEI1cekoqqeRZgEmRkgB/DBQQZDzXyknYU hoge@fuga-MacBook-Pro.local
The key's randomart image is:
+---[RSA 3072]----+
|&@@+o++=oo. |
|*=.=+E++*o.. |
| ...oo.ooo= |
|. o. . .+ o |
| o.. S . |
| .. |
|. . |
|. o |
|oo |
+----[SHA256]-----+無事作られると、カレントディレクトリに id_rsa_test、および id_rsa_test.pub が作成されます。
$ ls
id_rsa_test id_rsa_test.pubここで、id_rsa_testが秘密鍵、id_rsa_test.pub が公開鍵です。先程のRSA暗号の説明によれば、秘密鍵の方に認証に使う数 \(d\) の情報があるはずです。実はもっと詳しく、素因数分解に使われる素数の情報がid_rsa_test には書かれているため、確認しておきましょう。
まず、id_rsa_test はopenSSH形式になっているため、一旦PEM形式に変換して内容を確認してみます。
# 元のファイルをバックアップ
cp id_rsa_test{,.org}
# PEM形式に変換
ssh-keygen -p -m PEM -f id_rsa_test
# opensslコマンドで内容を確認
openssl rsa -in id_rsa_test -text -noout最後のコマンドを実行すると、次のような出力が表示されます。この中のprime1、prime2が実際に使われている素数です。
$ openssl rsa -in id_rsa_test -text -noout
Private-Key: (3072 bit, 2 primes)
~~~
prime1:
00:c9:53:cc:58:b5:ad:e9:03:88:32:93:bd:a0:2a:
3d:4c:a4:0a:1e:39:a4:4e:3c:c0:f1:d5:a3:5f:25:
a4:33:a2:dc:65:13:e2:3c:8c:57:d2:51:29:db:eb:
15:65:17:6e:84:cc:e4:a3:d4:b1:8d:a5:ff:ac:00:
ee:a2:bf:69:5f:c6:a2:95:39:a5:5c:43:2b:35:78:
fb:1c:bf:71:f3:5e:63:97:c9:c5:d6:d1:5c:fa:b5:
a4:8f:e5:93:50:cf:77:bb:32:e4:f6:92:4d:f4:af:
5d:32:0f:9a:be:0c:41:5b:9e:cf:8d:58:c4:df:f0:
4b:12:b7:65:33:51:a6:49:48:71:45:3c:1f:62:64:
f9:14:f6:cf:1a:d4:e8:07:f8:ba:a8:a1:c0:df:f6:
ec:c7:d2:e9:7d:3c:7f:9b:7a:dc:aa:a2:d3:37:97:
62:69:8a:ab:81:45:50:71:ab:b7:b9:ae:7f:93:7e:
f4:a2:56:84:d2:5a:bc:b1:fd:9a:04:cc:4d
prime2:
00:c1:8e:b9:cc:6d:ba:a1:50:12:d4:ca:7c:57:19:
1d:07:04:0b:08:e9:3a:fa:ef:49:cf:ad:b3:73:f9:
fa:67:92:25:a8:55:e3:d9:46:f1:60:35:76:42:c3:
e9:ad:c4:65:f5:98:5f:40:17:56:f1:a1:29:b6:94:
a8:b2:e1:42:4e:c9:97:6a:0e:2c:19:83:f4:3a:2c:
cc:21:d1:0e:08:de:30:fb:2a:b0:43:8e:8c:42:3c:
d1:bb:a6:78:f6:81:95:fe:3f:13:ef:10:35:9b:bd:
09:69:31:91:2e:d3:61:cd:6e:59:de:59:3f:2d:17:
d2:ac:bb:f6:a5:65:65:8c:7a:93:ad:47:67:48:03:
44:f7:65:a8:6f:b0:e6:63:8c:ed:96:20:75:51:31:
49:86:a6:60:ac:3d:72:3c:a4:f4:51:f4:32:19:10:
8a:e7:59:f1:ff:69:ed:d9:cf:69:8e:55:c5:81:e9:
2e:d6:25:e7:12:aa:75:32:25:02:91:55:63上記は16進数表記なので、10進数表記も確認しておきましょう。
prime1 の方を別ファイル (prime1.txt) に書き込んで保存します。その後、以下のコマンドを実行します。
cat prime1.txt | tr -d ' \t\n:' | python3 -c "importsys;print(int(sys.stdin.read().strip(),16))"; echoこれを実行すると、以下の数を得ることができます。
$ cat prime1.txt | tr -d ' \t\n:' | python3 -c "import sys;print(int(sys.stdin.read().strip(),16))"; echo
1895553835318037634169253034079462519995250654486080491122055522955203140497718879334014198489917095154410142467103075222442252780206491991716770794523898741244373905183798586676381728595612483849969589547523864744063785831800562125530883956836337795741853836758351815572421011478129329703423490525614654647351023845783468474312979144234342062176761853665178922304710312296419167629748691521621121860059630675742168709300643472884591315744572121984947012694756429最後に表示された長い数が、prime1として使われている素数です。これが素数かどうかの判定を自力でするのは難しいですが、以下のサイトでは桁数1000までの数の素数判定ができます(試してみると、実際に素数であることが確認できました)
公開鍵の配置と鍵認証によるSSH接続
それでは公開鍵を作成したコンテナに配置して、鍵認証によってSSH接続してみましょう。まず、先程確認のためにPEM形式に変換した秘密鍵を削除して、バックアップしておいた秘密鍵をリネームします。
# PEM形式のファイルを削除
rm id_rsa_test
# バックアップしておいたファイルを元のファイル名にリネーム
mv id_rsa_test{.org,}次に、公開鍵の情報をコンテナ側に書き込みます。以下のコマンドを実行してください。
ssh-copy-id -i id_rsa_test.pub -p 2222 test-user@localhost実行すると、test-userのパスワードを聞かれるので、入力します。
$ ssh-copy-id -i id_rsa_test.pub -p 2222 test-user@localhost
/usr/bin/ssh-copy-id: INFO: Source of key(s) to be installed: "id_rsa_test.pub"
/usr/bin/ssh-copy-id: INFO: attempting to log in with the new key(s), to filter out any that are already installed
/usr/bin/ssh-copy-id: INFO: 1 key(s) remain to be installed -- if you are prompted now it is to install the new keys
test-user@localhost's password:
Number of key(s) added: 1
Now try logging into the machine, with: "ssh -i ./id_rsa_test -p 2222 'test-user@localhost'"
and check to make sure that only the key(s) you wanted were added.これで準備が整ったので、鍵認証でSSH接続してみましょう。以下のコマンドを実行して、リモート側のプロンプトが表うじされればOKです。
ssh -p 2222 -i id_rsa_test test-user@localhost以下、実行結果です。
$ ssh -p 2222 -i id_rsa_test test-user@localhost
Last login: Tue Nov 11 04:46:26 2025 from 172.17.0.1
[test-user@bb4e15717701 ~]$これにて、鍵認証によるリモートへのSSH接続設定が完了しました。セキュリティ的には、このあとパスワード認証を無効化したりなどありますが、今回はここまでで作業終了とします。
まとめ
今回は暗号周りのことをおさらいし、RSA暗号を用いた公開鍵暗号方式の説明と実践について解説しました。これらのことは業務上当たり前のように出てくるので、実際に使うコマンドだけでなく裏でどういうことが行われているかを理解するのは非常に大事なことだと考えています。
この記事を書くにあたり、以下の本を参考にしています。暗号の歴史から数学の少し踏み込んだ話まで書かれているため、更に詳しく知りたい方はご一読ください。
今回のことが少しでも皆様にお役に立てれば幸いです。それでは、ここまでよんでいただきありがとうございました。
- 暗号は古くから使われており、以下が代表的な暗号。
- シーザー暗号
- 換字式暗号
- ヴィジュネル暗号
- エニグマ暗号
- 鍵配送の問題を解決するため、公開鍵暗号方式が生まれた。
- 公開鍵暗号方式は秘密鍵と公開鍵という2つの鍵を用いる。
- 秘密鍵と公開鍵の生成にはRSA暗号を始め、いろいろな生成方法がある。
- RSA暗号は、素因数分解の困難さで安全性を担保している。












