この記事では、線形代数学において中心的役割を担う線形空間と線形写像について解説します。これらの概念は、前回説明した行列やベクトルよりも更に抽象的な概念になるので、最初学ぶときはかなり戸惑う人が多いと思います。
ITの世界においても、線形空間や線形写像を用いて各種技術の説明をしている本や記事がたくさんあるので、それらを理解することの一助になれば幸いです。
今回の内容に入る前に、行列やベクトルがよく分かっていないという方は、以下の記事を参照していただければ。
- 線形空間と線形写像の定義
- 線形写像 (回転変換と拡大・縮小変換) のPythonを用いた可視化
線形空間
まず、線形空間とは大雑把に言うと「曲がっていない真っ直ぐな空間」です。例としては
- \(\mathbb{R}^2\)自身、および\(\mathbb{R}^2\) における原点を通る直線
- \(m\times n\)型行列全体の集合 \(\mathrm{M}(m;n)\)
- 斉次連立一次方程式の解空間
- \(\mathbb{R}\) 上定義された実数値関数全体の集合
などが挙げられます。ITの世界においては数ベクトルを扱う場合が多いので、1つ目の例が重要になってきます。
これらの集合に共通していることは
- 集合に属する2つ元について、それらの加法もその集合に属する
- 集合に属する元の定数倍も、やはりその集合に属する
ということが成り立っており、さらに加法や定数倍における結合律、分配律なども成り立ちます。
つまり、線形空間はこういった比較的扱いやすい「線形的な対象」の集合を抽象化した概念ということができ、このあとの正式な定義でも実際にその様になっています。
線形空間はベクトル空間とも呼ばれています。どちらの用語を使うかは記事や本の著者の好みになりますが、両者は同じ対象を指していることを認識しておけばOKです。
線形空間の定義と例
それでは早速線形空間の正式な定義を書きます。また、この記事では実線形空間のみ扱います。
集合 \(V\) に加法 \(+\) と各元に対する実数の定数倍が定義され、次の条件を満たすとき \(V\) を(実)線形空間、もしくは(実)ベクトル空間という: 任意の \(\boldsymbol{ x },\ \boldsymbol{ y },\ \boldsymbol{ z } \in V\) および \(a,\ b \in \mathbb{R}\) に対して以下が成り立つ。
- \((\boldsymbol{ x }+\boldsymbol{ y })+\boldsymbol{ z } = \boldsymbol{ x } + (\boldsymbol{ y } + \boldsymbol{ z }) \hspace{2mm} (\text{結合律})\)
- \(\boldsymbol{ x } + \boldsymbol{ y } = \boldsymbol{ y } + \boldsymbol{ x } \hspace{2mm} (\text{交換律}) \)
- 零ベクトルとよばれる元 \(\boldsymbol{ 0 }\) が存在して \(x + \boldsymbol{ 0 } = \boldsymbol{ 0 } + x = x \hspace{2mm} (\text(加法における単位元の存在))\)
- \((a+b)\boldsymbol{ x } = a\boldsymbol{ x } + b \boldsymbol{ x }\)
- \(a(\boldsymbol{ x } + \boldsymbol{ y }) = a \boldsymbol{ x } + a \boldsymbol{ y }\)
- \((ab)\boldsymbol{ x } = a(b\boldsymbol{ x })\)
- \(1\boldsymbol{ x } = \boldsymbol{ x }\)
次に、冒頭で紹介した \(\mathbb{R}^2\) が線形空間であることを証明してみます。ただ、今後のことを考えて、まず以下の命題を証明します。
線形空間 \(V,\ W\) に対してそれらの直積集合 \(V \times W\) は、以下の加法と定数倍に関して線形空間になる: \((\boldsymbol{ v }_1, \boldsymbol{ w }_1),\ (\boldsymbol{ v }_2, \boldsymbol{ w }_2) \in V \times W \)、\(a \in \mathbb{R}\) に対して
\begin{flalign*}
&(\boldsymbol{ v }_1, \boldsymbol{ w }_1) + (\boldsymbol{ v }_2, \boldsymbol{ w }_2) = (\boldsymbol{ v }_1 + \boldsymbol{ v }_2, \boldsymbol{ w }_1 + \boldsymbol{ w } _2),\\
& a (\boldsymbol{ v }_1 , \boldsymbol{ w }_1) = (a\boldsymbol{ v }_1 , a\boldsymbol{ w }_1).
\end{flalign*}
直積集合とは、それぞれの集合の元同士のペアリング全体の集合です。つまり、上記の \(V \times W\) の定義としては以下になります:
\[
V \times W := \{(\boldsymbol{ v },\boldsymbol{ w })\ |\ \boldsymbol{ v } \in V,\ \boldsymbol{ w } \in W\}
\]
命題内に記載の加法と定数倍が定義されることは自明なため、定義に記載の7つの条件を確かめる。
任意に \((\boldsymbol{ v }_1, \boldsymbol{ w }_1), (\boldsymbol{ v }_2, \boldsymbol{ w }_2),\ (\boldsymbol{ v }_3,\ \boldsymbol{ w }_3) \in V \times W\)、および \(a,\ b \in \mathbb{R}\)を取る。このとき、線形空間 \(V,\ W\) が加法の結合律、交換律を満たすことより以下が分かる:
\begin{flalign*}
((\boldsymbol{ v }_1, \boldsymbol{ w }_1) + (\boldsymbol{ v }_2, \boldsymbol{ w }_2)) + (\boldsymbol{ v }_3, \boldsymbol{ w }_3) &= (\boldsymbol{ v }_1 + \boldsymbol{ v }_2, \boldsymbol{ w }_1 + \boldsymbol{ w }_2) + (\boldsymbol{ v }_3, \boldsymbol{ w }_3) \\
&= ((\boldsymbol{ v }_1 + \boldsymbol{ v }_2) + \boldsymbol{ v }_3 , (\boldsymbol{ w }_1 + \boldsymbol{ w }_2) + \boldsymbol{ w }_3) \\
& = (\boldsymbol{ v }_1 + (\boldsymbol{ v }_2 + \boldsymbol{ v }_3)) , \boldsymbol{ w }_1 + (\boldsymbol{ w }_2 + \boldsymbol{ w }_3)) \\
& = (\boldsymbol{ v }_1, \boldsymbol{ w }_1) + ((\boldsymbol{ v }_2, \boldsymbol{ w }_2) + (\boldsymbol{ v }_3, \boldsymbol{ w }_3)),
\end{flalign*}
\begin{flalign*}
(\boldsymbol{ v }_1, \boldsymbol{ w }_1) + (\boldsymbol{ v }_2, \boldsymbol{ w }_2) &= (\boldsymbol{ v }_1 + \boldsymbol{ v }_2, \boldsymbol{ w }_1 + \boldsymbol{ w }_2) \\
&= (\boldsymbol{ v }_2 + \boldsymbol{ v }_1, \boldsymbol{ w }_2 + \boldsymbol{ w }_1)\\
&= (\boldsymbol{ v }_2, \boldsymbol{ w }_2) + (\boldsymbol{ v }_1, \boldsymbol{ w }_1).
\end{flalign*}
また、\((0,0) \in V \times W\) が加法における単位元であることも容易にわかる(余力のある方は証明してみてください)。
最後に、定数倍に関する性質を示す。任意の \((\boldsymbol{ v }_1, \boldsymbol{ w }_1), (\boldsymbol{ v }_2, \boldsymbol{ w }_2)) \in V \times W\) および \(a,\ b \in \mathbb{R}\) に対して \(V,\ W\) が線形空間であることから、以下が成り立つ:
\begin{flalign*}
(a+b)(\boldsymbol{ v }_1, \boldsymbol{ w }_1) &= ((a+b)\boldsymbol{ v }_1, (a+b)\boldsymbol{ w }_1)\\
&=(a\boldsymbol{ v }_1 + b \boldsymbol{ v }_1, a \boldsymbol{ w }_1 + b \boldsymbol{ w }_1) \\
&=(a \boldsymbol{ v }_1, a \boldsymbol{ w }_1) + (b \boldsymbol{ v }_1, b \boldsymbol{ w }_1) \\
&=a( \boldsymbol{ v }_1, \boldsymbol{ w }_1) + b(\boldsymbol{ v }_1, \boldsymbol{ w }_1),
\end{flalign*}
\begin{flalign*}
a((\boldsymbol{ v }_1, \boldsymbol{ w }_1) + (\boldsymbol{ v }_2, \boldsymbol{ w }_2)) &= a (\boldsymbol{ v }_1 + \boldsymbol{ v }_2 , \boldsymbol{ w }_1 + \boldsymbol{ w }_2) \\
&= (a(\boldsymbol{ v }_1 + \boldsymbol{ v }_2) , a(\boldsymbol{ w }_1 + \boldsymbol{ w }_2)) \\
&=(a\boldsymbol{ v }_1 + a\boldsymbol{ v }_2 , a\boldsymbol{ w }_1 + a\boldsymbol{ w }_2) \\
&=(a\boldsymbol{ v }_1 , a\boldsymbol{ w }_1) + (a\boldsymbol{ v }_2, a\boldsymbol{ w }_2) \\
&= a (\boldsymbol{ v }_1, \boldsymbol{ w }_1) + a (\boldsymbol{ v }_2, \boldsymbol{ w }_2) ,
\end{flalign*}
\begin{flalign*}
(ab)(\boldsymbol{ v }_1, \boldsymbol{ w }_1) &= ((ab)\boldsymbol{ v }_1, (ab)\boldsymbol{ w }_1) \\
&=(a(b\boldsymbol{ v }_1), a(b\boldsymbol{ w }_1))\\
&=a(b\boldsymbol{ v }_1, b\boldsymbol{ w }_1) \\
&=a(b(\boldsymbol{ v }_1, \boldsymbol{ w }_1) ),
\end{flalign*}
\begin{flalign*}
1(\boldsymbol{ v }_1, \boldsymbol{ w }_1) &=(1\boldsymbol{ v }_1, 1\boldsymbol{ w }_1)=(\boldsymbol{ v }_1, \boldsymbol{ w }_1).
\end{flalign*}
以上より、\(V \times W\) は線形空間であることが分かる。
上記命題および数学的帰納法を用いることにより、\(V_1,\ldots,V_n\) が線形空間であれば \(V_1 \times \cdots \times V_n\) も線形空間にであることが分かります。こちらについては興味がある方は証明を試みていただければと思います。
以上により\(\mathbb{R}^2\)、さらに自然数 \(n\) について \(\mathbb{R}^n\) が線形空間であることが分かります。
線形写像
線形写像を抽象的に説明すると「線形空間から線形空間への構造を保つ元の対応付け」になります。ここで「構造を保つ」とは、線形写像で対応付ける前に元同士を足したり定数倍した結果と、対応付けをした後に足したり定数倍したりした結果がいつでも同じになるという意味です。具体的な線形写像の例としては以下があります:
- ある \(n\) 次正方行列 \(A\) を用いて、\(F(\boldsymbol{ x }) = A\boldsymbol{ x }\) で定義される \(\mathbb{R}^n\) から\(\mathbb{R}^n\) への写像 \(F_A\).
- \(\mathbb{R}\) 上定義された無限回微分可能な関数全体の集合から各関数の1階導関数を返す写像 \(\frac{d}{dx}\).
上記の1つ目の写像 \(F_A\) は、固定された行列 \(A\) を縦ベクトルに掛けるという操作です。2つ目の写像は微分演算でありここでは詳しく触れませんが、これも線形写像の一つの例になっています。
それでは、線形写像の定義と例を見ていきましょう。
線形写像の定義と例
\(V,\ W\) を線形空間とする。写像 \(f \colon V \to W\) が線形写像であるとは、任意の \(\boldsymbol{ x },\ \boldsymbol{ y } \in V\) および \(a \in \mathbb{R}\) に対して、以下の2つの条件を満たすことである:
- \(f(\boldsymbol{ x } + \boldsymbol{ y }) = f (\boldsymbol{ x }) + f(\boldsymbol{ y })\)
- \(f(a \boldsymbol{ x }) = a f(\boldsymbol{ x })\)
この節の冒頭で説明した「構造を保つ」を定式化したので上記の定義になります。見て分かる通り、足したり定数倍したあとで送った結果と、送った後で足したり定数倍した結果が同じになっています。
数学の世界において、このように構造を保つ写像のことを準同型写像と呼びます。線形写像は線形空間の世界における準同型写像であり、他にも群の世界の群準同型、環の世界の環準同型などがあります。
送り元と送り先が全く同じ集合であるとき、線形写像は線形変換とも呼ばれます。
それでは、次に冒頭で紹介した1つ目の例が、実際に線形写像になっていることを確認してみましょう。実際に証明する命題は以下になります。
写像 \(F_A \colon \mathbb{R}^n \to \mathbb{R}^n;\ \boldsymbol{ x } \mapsto A \boldsymbol{ x }\) は\(\mathbb{R}^n\) から \(\mathbb{R}^n\) への線形写像である。
基本的に \(\mathbb{R}^n\) の各元は縦ベクトルで表しますが、証明中に毎回縦ベクトルを書くのは面倒です。そのため、ここでは行列の転置 \((\cdot)^{t}\) を導入して記法を簡素化します。
ここで新しく導入した転置とは、行列・ベクトルの行と列をひっくり返す操作のことです。具体的な計算例としては以下のとおりです。
$$
{}^t (1,2,3,4) =
\left(
\begin{array}{c}
1 \\
2 \\
3 \\
4
\end{array}
\right)
$$
任意に \(\boldsymbol{ x }={}^t\!(x_1, \ldots,x_n),\ \boldsymbol{ y } = {}^t\!(y_1,\ldots,y_n) \in \mathbb{R}^n\) および \(a \in \mathbb{R}\) を取る。また、 \(A = (a_{ij})_{ij}\) と表示しておく。このとき
$$
\begin{flalign*}
F_A(\boldsymbol{ x } + \boldsymbol{ y }) &= F_A({}^t(x_1+y_1,\ldots,x_n + y_n))\\
&=\left(
\begin{array}{ccc}
a_{11} & \cdots & a_{1n} \\
\vdots & & \vdots \\
a_{n1} & \cdots & a_{nn}
\end{array}
\right) \left(
\begin{array}{c}
x_1 + y_1 \\
\vdots \\
x_n + y_n
\end{array}
\right)\\
&=\left(
\begin{array}{c}
\dsum{n}{k=1}a_{1k}(x_k + y_k) \\
\vdots \\
\dsum{n}{k=1}a_{nk}(x_k + y_k)
\end{array}
\right) \\
&= \left(
\begin{array}{c}
\dsum{n}{k=1}a_{1k}x_k \\
\vdots \\
\dsum{n}{k=1}a_{nk}x_k
\end{array}
\right) +
\left(
\begin{array}{c}
\dsum{n}{k=1}a_{1k}y_k \\
\vdots \\
\dsum{n}{k=1}a_{nk}y_k
\end{array}
\right)\\
&= A \boldsymbol{ x } + A\boldsymbol{ y } = F_A(\boldsymbol{ x }) + F_A(\boldsymbol{ y })
\end{flalign*}
$$
であり、さらに
$$
\begin{flalign*}
F_A(a\boldsymbol{ x }) &= F_A({}^t(ax_1,\ldots.ax_n)) \\
&= \left(
\begin{array}{ccc}
a_{11} & \cdots & a_{1n} \\
\vdots & & \vdots \\
a_{n1} & \cdots & a_{nn}
\end{array}
\right) \left(
\begin{array}{c}
ax_1 \\
\vdots \\
ax_n
\end{array}
\right)\\
&= \left(
\begin{array}{c}
\dsum{n}{k=1}a_{1k}(ax_k) \\
\vdots \\
\dsum{n}{k=1}a_{nk}(ax_k)
\end{array}
\right) \\
&=
\left(
\begin{array}{c}
a\dsum{n}{k=1}a_{1k}x_k \\
\vdots \\
a\dsum{n}{k=1}a_{nk}x_k
\end{array}
\right) \\
&= aA\boldsymbol{ x } = aF_A(\boldsymbol{ x })
\end{flalign*}
$$
が分かる。以上により、 \(F_A\) は線形写像であることが証明された。
上記は、具体的な \(F_A\) という写像が線形写像であるという命題ですが、実は逆の主張も成り立ちます。
写像 \(F \colon \mathbb{R}^n \to \mathbb{R}^n\) が線形写像であるための必要十分条件は、\(n\)次正方行列 \(A\) が存在して \(F=F_A\) となることである。
\(F \colon \mathbb{R}^n \to \mathbb{R}^n\) が線形写像であることを仮定する。ある行列 \(A\) が存在して \(F=F_A\) となることを示す。まず、以下のように第\(i\) 行目が \(1\) であるベクトルを次の記号で表す:
$$
\boldsymbol{ e }_i :={}^t(0,\ldots,0,1,0,\ldots,0).
$$
このとき、上記ベクトルの \(F\) による送り先を並べた行列を \(A\) とする。つまり以下の行列
\(A\) を考える:
$$
A := (F(\boldsymbol{ e }_1),\ldots,F(\boldsymbol{ e }_n))) := \left(
\begin{array}{ccc}
a_{11} & \cdots & a_{1n} \\
\vdots & & \vdots \\
a_{n1} & \cdots & a_{nn}
\end{array}
\right)
$$
ここで、 \(F(\boldsymbol{ e }_i) := {}^t(a_{1i},\ldots,a_{ni}) \) と置いたことに注意する。
以下、\(F=F_A\) であることを示す。そのためには、任意のベクトル \(\boldsymbol{ x }={}^t(x_1,\ldots,x_n) \in \mathbb{R}^n\) に対して、\(F(\boldsymbol{ x }) = F_A(\boldsymbol{ x })\) となることを証明すれば良い。ベクトル \(\boldsymbol{ x }={}^t(x_1,\ldots,x_n) \in \mathbb{R}^n\) は \(\boldsymbol{ e }_i \ (1 \leq i \leq n)\) を使って
$$
\boldsymbol{ x } = \dsum{n}{i=1}x_i\boldsymbol{ e }_i
$$
と書けることに注意すると、\(F\) が線形写像であることから
$$
\begin{flalign*}
F(\boldsymbol{ x }) = F\left(\dsum{n}{i=1}x_i\boldsymbol{ e }_i\right) = \dsum{n}{i=1}x_iF(\boldsymbol{ e }_i) &= \dsum{n}{i=1}x_i {}^t(a_{1i},\ldots,a_{ni})\\
&= \left(\dsum{n}{i=1}a_{1i}x_i ,\ldots, \dsum{n}{i=1}a_{ni}x_i\right)
\end{flalign*}
$$
が分かる。また、上記の最後の式は、行列の積として以下のように変形できる:
$$
\left(\dsum{n}{i=1}a_{1i}x_i ,\ldots, \dsum{n}{i=1}a_{ni}x_i\right)=\left(
\begin{array}{ccc}
a_{11} & \cdots & a_{1n} \\
\vdots & & \vdots \\
a_{n1} & \cdots & a_{nn}
\end{array}
\right) \left(
\begin{array}{c}
x_1 \\
\vdots \\
x_n
\end{array}
\right) = F_A(\boldsymbol{ x })
$$
以上より、任意の \(\boldsymbol{ x } \in \mathbb{R}^n\) に対して \(F(\boldsymbol{ x }) = F_A(\boldsymbol{ x })\) が証明されたため、\(F=F_A\) である。
逆の主張についてはすでに証明済みのため、以上で題意が示された。
この主張はかなり重要で、\(\mathbb{R}^n\) 上の線形写像は実質的に行列として扱っても差し支えないことが分かります。このように線形写像に対応する行列を、その写像の表現行列と呼びます。ただし、上記の行列 \(A\) は \(\boldsymbol{ e }_i\) たちの行き先を並べたものになるので、写像 \(F\) だけの情報から定まっているわけではないことに注意が必要です。そのため、上記の行列 \(A\) は \(F\) に対して一意的に定まるわけではないため、正確には 基底 \((\boldsymbol{ e }_1,\ldots,\boldsymbol{ e }_n)\) に関する表現行列と呼びます。「基底とは何か」については、次回以降の記事で解説したいと思います。
線形写像の可視化
ここまで抽象的な議論が続いたので、実際に線形写像を可視化してみましょう。今まで見てきた通り、 \(\mathbb{R}^n\) 上の線形写像は実質的には行列をベクトルに掛けることで表すことができますが、ここでは \(\mathbb{R}^2\) から \(\mathbb{R}^2\) への線形写像の内、よく使われるものを可視化してみます。
ベクトルの回転
ベクトルの回転はよく使われる操作の一つであり、これは行列で表すことができます。具体的には、座標平面上において、原点を中心として左回りに角度 \(\theta\) だけ回転させる行列は以下です:
$$
R(\theta):=\left(
\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}
\right)
$$
上記行列を使って、ベクトルを回転させてみましょう。以下のコードを手元で実行してみてください。
import numpy as np
import matplotlib.pyplot as plt
# ベクトルを描画するための関数の設定
def draw_vector(loc, vector, color):
plt.quiver(
loc[0],
loc[1],
vector[0],
vector[1],
color=color,
angles="xy",
scale_units="xy",
scale=1,
)
# 回転行列
def rotate_matrix(rad):
rotate = np.array([[np.cos(rad), -np.sin(rad)], [np.sin(rad), np.cos(rad)]])
return rotate
# ベクトルの回転
def rotate_vector(vector, rotate_matrix):
rotated_vector = np.matmul(rotate_matrix, vector)
return rotated_vector
# 回転させるベクトルの入力
print("回転させるベクトルを入力してください (例: (1,2) であれば 1 2 と入力)")
vector = list(map(float, input().split()))
# 回転させる角度
print("回転させる角度を入力してください (例: 30 度の場合 30)")
angle = int(input())
# 入力した角度を弧度法に変換
rad = np.radians(angle)
# 入力したベクトルを array に変換
vector_array = np.array([[vector[0]], [vector[1]]])
draw_vector([0, 0], vector_array, "red")
draw_vector([0, 0], rotate_vector(vector_array, rotate_matrix(rad)), "blue")
# ベクトルへのラベル付け
plt.text(vector_array[0], vector_array[1], "before")
plt.text(
rotate_vector(vector_array, rotate_matrix(rad))[0],
rotate_vector(vector_array, rotate_matrix(rad))[1],
"after",
)
# 描画範囲の設定
axis_lim = (
max(
abs(vector_array[0]),
abs(vector_array[1]),
abs(rotate_vector(vector_array, rotate_matrix(rad))[0]),
abs(rotate_vector(vector_array, rotate_matrix(rad))[1]),
)
+ 1
)
plt.xlim(-axis_lim, axis_lim)
plt.ylim(-axis_lim, axis_lim)
plt.grid(color="b", linestyle=":", linewidth=0.3)
plt.show()
実行すると、回転する角度と回転させるベクトルの入力が求められます。例えば、回転角度が30度で回転させるベクトルを (1, 0) とすると、次の画像が生成されます:
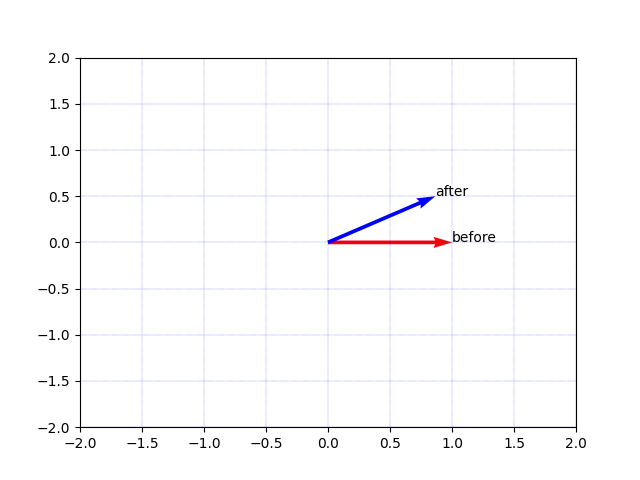
拡大・縮小
ベクトルの拡大縮小もよく使われます。こちらの操作を表現する行列は先程の回転よりも簡単な形をしていて、以下になります:
$$
\left(
\begin{array}{cc}
c & 0 \\
0 & c \\
\end{array}
\right) \hspace{2mm} (c \ne 0)
$$
ここで、定数 \(c\) はどれくらい拡大・縮小するかの比率です。\( 0 < |c| < 1\) であればベクトルを縮小し、\(|c| > 1\) であればベクトルを拡大します (もちろん \(|c|=1\) の場合はベクトルの大きさは変わりません)。
それではこちらもPythonで描画してみましょう。以下のコードを実行してみてください。
import numpy as np
import matplotlib.pyplot as plt
# ベクトルを描画するための関数の設定
def draw_vector(loc, vector, color):
plt.quiver(
loc[0],
loc[1],
vector[0],
vector[1],
color=color,
angles="xy",
scale_units="xy",
scale=1,
)
# 拡大・縮小行列
def sim_matrix(ratio):
similar = np.array([[ratio, 0], [0, ratio]])
return similar
# ベクトルの拡大・縮小
def sim_vector(vector, sim_matrix):
vector = np.matmul(sim_matrix, vector)
return vector
# 拡大・縮小させるベクトル
print("拡大・縮小させるベクトルを入力してください (例: (1,2) であれば 1 2 と入力)")
vector = list(map(float, input().split()))
# 拡大率
print("ベクトルの拡大率を入力してください")
ratio = int(input())
# 入力したベクトルを array に変換
vector_array = np.array([[vector[0]], [vector[1]]])
draw_vector([0, 0], vector_array, "red")
draw_vector([0, 0], sim_vector(vector_array, sim_matrix(ratio)), "blue")
# ベクトルへのラベル付け
plt.text(vector_array[0], vector_array[1], "before")
plt.text(
sim_vector(vector_array, sim_matrix(ratio))[0],
sim_vector(vector_array, sim_matrix(ratio))[1],
"after",
)
# 描画範囲の設定
axis_lim = (
max(
abs(vector_array[0]),
abs(vector_array[1]),
abs(sim_vector(vector_array, sim_matrix(ratio))[0]),
abs(sim_vector(vector_array, sim_matrix(ratio))[1]),
)
+ 1
)
plt.xlim(-axis_lim, axis_lim)
plt.ylim(-axis_lim, axis_lim)
plt.grid(color="b", linestyle=":", linewidth=0.3)
plt.show()
実行すると、拡大・縮小するベクトルと拡大・縮小率の入力が求められます。例えば、拡大・縮小するベクトルを (1, 2) として拡大・縮小率を -2 とすると、次の画像が生成されます:
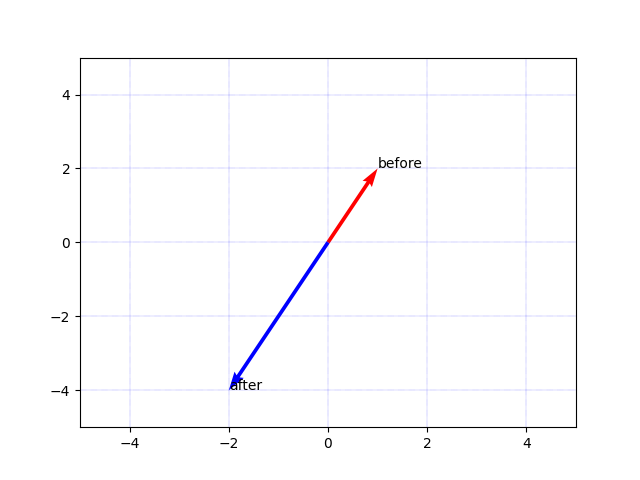
まとめ
今回は線形空間と線形写像の定義と簡単な性質を確認し、線形写像についてはPythonを用いて可視化してみました。今流行りのAIに関しては線形代数学がふんだんに使われているので、そちらの方面に興味がある方は線形空間や線形写像に慣れておくと良いと思われます。
- 線形空間、線形写像の定義と簡単な性質の確認
- 線形空間の直積が線形空間になること
- \(\mathbb{R}^n\) から \(\mathbb{R}^n\) への線形写像が本質的に行列で表されること
- 線形写像のPythonを用いた可視化











