線形代数学は、数学のみならず工学や物理学、最近だと機械学習等に幅広く利用されている学問です。線形代数学を学ぶことで、複雑な事象を線形的な対象(行列やベクトルなど)で取り扱うことができ、見通しよく対象の分析が可能になります。
本記事では、線形代数学の基本となる行列とベクトルの定義と、定義される演算について扱います。特に、Pythonを用いた計算を行いながら説明するので、比較的わかりやすい記事になっています。Pythonの環境が構築されている方は、是非手を動かしながら本記事を御覧ください。
また、将来的には機械学習の解説を投稿したいと考えているので、線形代数学の各概念が機械学習の分野のどの概念に当てはまるかということも補足として書いています。
前提
- この記事では、行列やベクトルは実数の範囲で扱います。
- \(\mathbb{R}\)で実数全体の集合を表します。
ベクトル・行列の定義
まず、線形代数学の基礎となるベクトルと行列について解説します。
ベクトル
高校数学的に解説するなら、ベクトルとは位置を無視した大きさと向きを持った概念のことをベクトルと呼びます。具体例としては
- 物理学において、物体の速度を表す速度ベクトル
- 2次元平面内において、原点から各点に伸びる位置ベクト
- 機械学習におけるデータや特徴量の組
よく使われるベクトルをイメージとして理解するのであれば、ベクトルとは矢印のことです。高校数学・物理で使われるベクトルの多くは平面・空間ベクトルで、矢印で表したと思います。
上記説明はあくまでイメージ的に理解するためのラフな説明です。平面・空間ベクトルをきちんと定義するのであれば、平面・空間内の有向線分全体を考えて、それらを「平行移動で重なるものは同じとみなす」という同値関係による商集合の各元を平面・空間ベクトルとよびます。
ベクトルの抽象的な定義としては「線形空間に属する各要素」になりますが、こちらについては本記事では触れません。また、ベクトルについてはイメージがしやすい数ベクトルを扱い、特に標準的に使われている列ベクトル(数を1列に並べたもの)で以下説明していきます:
\[
\left(
\begin{array}{c}
1 \\
0
\end{array}
\right),\hspace{2mm}
\left(
\begin{array}{c}
2 \\
1 \\
3
\end{array}
\right).
\]
特に、上記の前者のような2つ数を並べたものを平面ベクトル、後者のような3つ数を並べたものを空間ベクトルと呼びます。一般に、数を \(n\) 個並べたベクトルを \(n\) 次元ベクトルと呼びます。
行列の定義
行列とは、数を長方形上に並べたもののことです。具体例としては以下のような対象を行列とよびます:
\[
\left(
\begin{array}{cc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} \\
\frac{1}{2} & \frac{\sqrt{3}}{2}
\end{array}
\right),\hspace{2mm}
\left(
\begin{array}{cc}
1 & 2\\
3 & 4
\end{array}
\right), \hspace{2mm}
\left(
\begin{array}{ccc}
1 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right)
\]
行列を用いることで、図形やベクトルの回転や移動という変換を表現できます。
行列では、その行数と列数を取り出して \(m \times n\) 型の行列などと呼びます。例えば、上記の最初の行列は \(2 \times 2\) 型、2つ目の行列は \(2 \times 3\) 型です。
一般の \(m \times n\) 型行列は次のように書かれます:
\[
\left(
\begin{array}{ccc}
a_{11} & \cdots & a_{1n} \\
\vdots & & \vdots \\
a_{m1} & \cdots & a_{mn}
\end{array}
\right)
\]
さらに、\(m \times n\) 型行列全体の集合を \(\mathrm{M}(m;n)\) と書きます。
ベクトル・行列の演算
ここでは、ベクトル同士、行列同士の間に定義される演算について解説します。
ベクトルの演算
ここではベクトルにおける加法、定数倍を定義します。扱うベクトルはすべて数ベクトルです。
ベクトルの加法
2つのベクトルの加法は成分同士の加法で定義します。つまり、\(n\) 次元ベクトル \(a = (a_i)_i\) および \(b = (b_i)_i\) に対して
\[
a + b =
\left(
\begin{array}{c}
a_1 \\
\vdots \\
a_n
\end{array}
\right) +
\left(
\begin{array}{c}
b_1 \\
\vdots \\
b_n
\end{array}
\right) =
\left(
\begin{array}{c}
a_1 + b_1 \\
\vdots \\
a_n + b_n
\end{array}
\right)
\]
と定義します。具体的な計算としては以下のとおりです:
\[
\left(
\begin{array}{c}
2 \\
1
\end{array}
\right) +
\left(
\begin{array}{c}
1 \\
3
\end{array}
\right) =
\left(
\begin{array}{c}
3 \\
4
\end{array}
\right).
\]
上記計算をPythonを用いて実行してみましょう。今回はインタラクティブモードを用いて計算してみます。まず、ターミナルにおいて python3と入力し実行します。そうすると、以下のようにインタラクティブモードが開始されます。
$ python3
Python 3.9.21 (main, Aug 19 2025, 00:00:00)
[GCC 11.5.0 20240719 (Red Hat 11.5.0-5)] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> そのうえで、以下のようにコマンドを実行します。ここで、各行ごとにエンターキーを押してください。
>>> import numpy as np
>>> u = np.array([[2],[1]])
>>> v = np.array([[1],[3]])
>>> u + v
array([[3],
[4]])最後の出力が、行列同士の足し算を実行した結果になります。ここで、いくつかの注意をしておきます。
import numpy as np- numpyというライブラリをインポートして、呼び出すときの名前を「np」に設定しています。ちなみに「numpy」は「ナムパイ」と発音します。
- np.array
- numpyライブラリ内のarray関数を呼び出します。これは、行列を定義するときに使います。
さて、せっかくなのでPythonを用いて上記のベクトルを可視化してみます。使うライブラリは引き続きnumpyと、追加でmatplotlibにおけるpyplotというものを使います。次のコードを実行してみてください。
import numpy as np
import matplotlib.pyplot as plt
def draw_vector(loc, vector, color):
plt.quiver(
loc[0],
loc[1],
vector[0],
vector[1],
color=color,
angles="xy",
scale_units="xy",
scale=1,
)
# ベクトルを定義
u = np.array([[2], [1]])
v = np.array([[1], [3]])
w = np.array([[3], [4]])
draw_vector([0, 0], u, "red")
draw_vector([0, 0], v, "blue")
draw_vector([0, 0], w, "green")
plt.xlim(-0.5, 4.5)
plt.ylim(-0.5, 4.5)
plt.grid(color="b", linestyle=":", linewidth=0.3)
plt.show()
実行すると、以下のような画像が表示されます。表示されている青のベクトルが \(x\) 座標が1, \(y\) 座標が3のベクトル、赤のベクトルが \(x\) 座標が2、\(y\) 座標が1のベクトルです。そして、それらを足したベクトルが緑のベクトルで、\(x\) 座標が3、\(y\) 座標が4 になります。
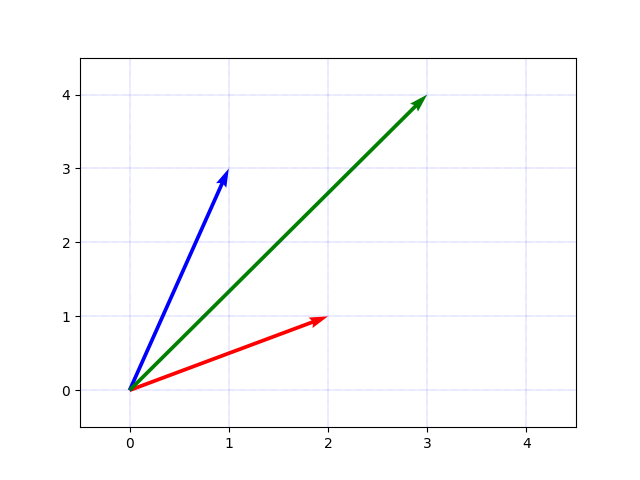
なぜ青と赤のベクトルを足すと緑のベクトルになるかというと、以下のように平行移動して青のベクトルの始点を赤のベクトルの終点に持っていくことで理解できます。
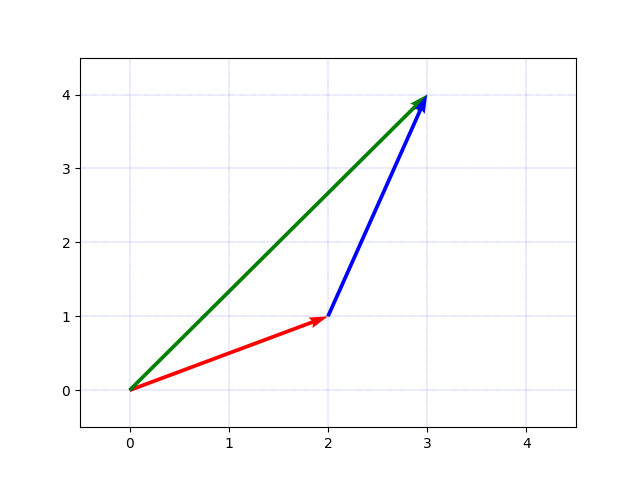
つまり、ベクトルの加法を図形的に見ると、足すベクトルたちを(平行移動をしながら)繋いでいって、最終的に到達する点と始点を結んだベクトルが加法の結果として得られるベクトルです。
上記説明の内、ベクトルを平行移動してよいのかという疑問があるかもしれません。しかし、ここで説明している平面ベクトルの定義は、平面内の有向線分全体の集合を、平行移動をして重なり合うものは同じと見做すという同値関係で割った商集合の各元のことです。これにより、ベクトル自体は平行移動しても全く問題ありません。
ちなみに、2つ目の図は上に提示したコードを修正することで得ることができます。こちらについてもどうやれば2つ目の図を出力できるか考えてみるとよいでしょう。以下に解答を載せておくので、チャレンジしてみてください。
import numpy as np
import matplotlib.pyplot as plt
def draw_vector(loc, vector, color):
plt.quiver(
loc[0],
loc[1],
vector[0],
vector[1],
color=color,
angles="xy",
scale_units="xy",
scale=1,
)
# ベクトルを定義
u = np.array([[2], [1]])
v = np.array([[1], [3]])
w = np.array([[3], [4]])
draw_vector([0, 0], u, "red")
# draw_vector([0, 0], v, "blue")
draw_vector([0, 0], w, "green")
# 以下を追加
draw_vector(u, v, "blue")
plt.xlim(-0.5, 4.5)
plt.ylim(-0.5, 4.5)
plt.grid(color="b", linestyle=":", linewidth=0.3)
plt.show()
ベクトルの定数倍
ベクトルを構成する各要素を定数倍することで、ベクトルの定数倍を定義できます。つまり、\(n\) 次元ベクトル \(a = (a_i)_i\) と \(c \in \mathbb{R}\) に対して
\[
ca =
c\left(
\begin{array}{c}
a_1 \\
\vdots \\
a_n
\end{array}
\right) =
\left(
\begin{array}{c}
ca_1 \\
\vdots \\
ca_n
\end{array}
\right)
\]
と定義します。具体的な計算としては以下のとおりです:
\[
2\left(
\begin{array}{c}
2 \\
1
\end{array}
\right) =
\left(
\begin{array}{c}
4 \\
2
\end{array}
\right).
\]
Pythonで計算をすると以下のようになります。
>>> import numpy as np
>>> u = np.array([[2],[1]])
>>> 2* u
array([[4],
[2]])こちらも図に表すと次のようになります。これを見ると分かるように、ベクトルの定数倍は方向自体は変えずに元のベクトルを伸ばしたり縮めたり(あるいは180度反対にしたり)したベクトルになります。
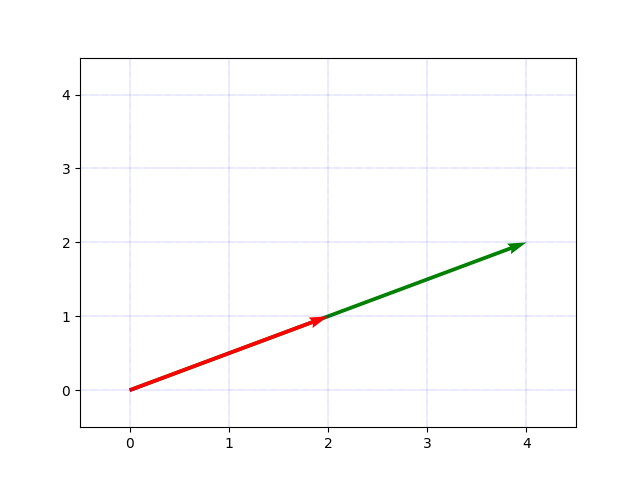
行列の演算
ここでは行列における加法、定数倍、乗法という演算を定義します。
行列の加法
まず行列同士の加法については、同じ型の行列同士において、各成分を足すことで定義します。\(A=(a_{ij})_{ij},\ B=(b_{ij})_{ij} \in \mathrm{M}(m;n)\) に対して
\[
A + B =\left(
\begin{array}{ccc}
a_{11} & \cdots & a_{1n} \\
\vdots & & \vdots \\
a_{m1} & \cdots & a_{mn}
\end{array}
\right) +
\left(
\begin{array}{ccc}
b_{11} & \cdots & b_{1n} \\
\vdots & & \vdots \\
b_{m1} & \cdots & b_{mn}
\end{array}
\right) =
\left(
\begin{array}{ccc}
a_{11}+b_{11} & \cdots & a_{1n} + b_{1n} \\
\vdots & & \vdots \\
a_{m1}+b_{m1} & \cdots & a_{mn}+b_{mn}
\end{array}
\right)
\]
と定義します。計算の具体例としては次のとおりです。
\[
\left(
\begin{array}{ccc}
1 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right) +
\left(
\begin{array}{ccc}
2 & -1 & 10 \\
0 & 3 & 0
\end{array}
\right) =
\left(
\begin{array}{ccc}
3 & 0 & 10 \\
0 & 3 & 1
\end{array}
\right).
\]
以下は、上記計算をPythonで実行した結果です:
>>> import numpy as np
>>> a = np.array([[1,1,0],[0,0,1]])
>>> b = np.array([[2,-1,10],[0,3,0]])
>>> a + b
array([[ 3, 0, 10],
[ 0, 3, 1]])行列の定数倍
行列の定数倍は、各成分を定数倍することで定義します。つまり、 \(m\times n\) 型行列 \(A\) と定数 \(c \in\mathbb{R}\) について、
\[
cA=c \left(
\begin{array}{ccc}
a_{11} & \cdots & a_{1n} \\
\vdots & & \vdots \\
a_{m1} & \cdots & a_{mn}
\end{array}
\right) =
\left(
\begin{array}{ccc}
ca_{11} & \cdots & ca_{1n} \\
\vdots & & \vdots \\
ca_{m1} & \cdots & ca_{mn}
\end{array}
\right)
\]
と定義します。具体的な計算の例は以下になります:
\[
3\left(
\begin{array}{cc}
1 & 2\\
3 & 4
\end{array}
\right) =
\left(
\begin{array}{cc}
3 & 6\\
9 & 12
\end{array}
\right).
\]
これをPythonで実行すると次のようになります。
>>> import numpy as np
>>> A = np.array([[1,2],[3,4]])
>>> 3 * A
array([[ 3, 6],
[ 9, 12]])行列の乗法
行列の乗法については少し特殊で、\(m \times n\) 型行列と \(n \times l\) 型行列というように、2項演算の左に来る行列の列数と右に来る行列の行数が一致する場合にのみ定義します。式で書くと、\(A=(a_{ij})_{ij} \in \mathrm{M}(m;n)\) および \(B = (b_{ij})_{ij} \in \mathrm{M(n;l)}\) に対して
\[
AB=
\left(
\begin{array}{ccc}
a_{11} & \cdots & a_{1n} \\
\vdots & & \vdots \\
a_{m1} & \cdots & a_{mn}
\end{array}
\right)
\left(
\begin{array}{ccc}
b_{11} & \cdots & b_{1l} \\
\vdots & & \vdots \\
b_{n1} & \cdots & b_{nl}
\end{array}
\right) =
\left(
\begin{array}{ccc}
c_{11} & \cdots & c_{1l} \\
\vdots & & \vdots \\
c_{m1} & \cdots & c_{ml}
\end{array}
\right).
\]
ただし、各 \(c_{ij}\) は次の式で定義します:
\[
c_{ij} := \sum^{n}_{k=1} a_{ik}b_{kj} \hspace{2mm} (1 \leq i \leq m,\ 1 \leq j \leq n).
\]
計算結果として出てくる行列は \(m \times l\) 型行列になることに注意しましょう。計算の具体例としては以下のとおりです。
\[
\left(
\begin{array}{ccc}
3 & 0 & 10 \\
0 & 3 & 1
\end{array}
\right)
\left(
\begin{array}{c}
3 \\
1 \\
0
\end{array}
\right) =
\left(
\begin{array}{c}
9 \\
3
\end{array}
\right).
\]
これをPythonで計算すると、次のようになります。
>>> import numpy as np
>>> a = np.array([[3,0,10],[0,3,1]])
>>> b = np.array([[3],[-1],[0]])
>>> np.matmul(a,b)
array([[ 9],
[-3]])最後の np.matmul が実際に行列の積を計算しています。
行列の積を計算する際、数の計算と同じ用に「*」を使ってしまうと別の結果が返ってきます。numpyでの行列演算において「*」はアダマール積を表していて、基本的には同じ型同士の行列において、その各行列の成分同士の積を成分とする行列を返します。
まとめ
本記事では線形代数学の中でも基本となるベクトルと行列を定義し、加法や定数倍、行列については乗法を定義しました。今回は初歩的な概念の解説をしましたが、今後はより発展的な内容の解説も行う予定ですので、もしよければお付き合いいただければ幸いです。
- 平面ベクトル、空間ベクトルとは、平面・空間に描かれた矢印のこと
- 抽象的には線形空間における各元をベクトルと呼ぶ。
- 行列とは、数を長方形状に並べたもの。










